Understanding the Data: Statistics

Introduction

In this lesson, we will get started with some very basic statistical analysis. A statistic of data is just a summary of that data for humans and computers. Imagine you have a medical history of 2 million people from multiple hospitals, and you want to know which disease is worst among a set of diseases. Of course, you cannot go through all the 2 million people and keep comparing by yourself. With the help of statistics and good computational power, you can do it within hours. You can visualize the body temperature box plots and see that one disease causes more fever than the others.

Concepts of Statistics in Machine Learning

Statistics is a vast field of study very close to machine learning. The core mathematics of machine learning is all about statistics. So if you want to learn theoretical machine learning, you should have advanced statistics knowledge. We will walk you through some basic statistical knowledge that you will need for applied machine learning.

Probability theorem

In Mathematics, probability is the likelihood of an event. The probability of an event going to happen is 1 and for an impossible event is 0. In a domain or problem set, the sum of the probability of all the events that might happen is 1. And the probability of an event can never be negative.

Most of the time, we say that there is a 50-50 chance of raining today. What we mean is the probability of raining today is 0.5. And the probability of not raining is 0.5. In the event space, there are only two events that might happen in this domain. raining and not raining. Note that the sum of the probability of these two events is (0.5 + 0.5) = 1.

Now think of a rolling die. There are 6 faces of a die. So there could be 6 events of a rolling die. Thus event space is $E = {1, 2, 3, 4, 5, 6}$. If the die is normal, then each of these events will have an equal probability to occur. And the sum of the probability of events will always be 1. So each event will have a

$$\frac{total\ probability}{#\ of\ events} = 1/6$$

Understanding the Venn Diagram helps a lot to understand probability. For the two domains discussed above, the Venn diagrams are shown below:

All of these events were mutually exclusive. This means only one event can happen at a time. Of course, you cannot have a rainy and no-raining state at the same time. Or you cannot get a 1 and 6 from a single die roll. There can be mutually inclusive events as well.

Think of guessing any number. That number can be a prime number (or not). That can also be a number less than 10 (or not). But can it be both prime and below 10? Yes, it can. So if we take events $E1 = {x: x < 10\ &\ x \in R}$ and $E2 = {x: x\ is\ prime}$, then $E1$ and $E2$ are mutually inclusive.

For mutually exclusive events $A$ and $B$, the probability of happening both events is zero.

$$P(A \cap B) = 0$$

But for mutually inclusive events, both of them can happen, so there is a probability of both events happening.

When we want to know the probability of two events happening, then we can use this formula:

$$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

Also, the probability of something not happening is the inverse of the probability of something happening.

$$P(A’) = 1 - P(A)$$

Probability Mass function and Density function

Probability mass function and density function are two functions in the world of probability calculus. Both of these are functions for a random variable. A random variable is a variable whose value is unknown or a function that assigns values to each of an experiment’s outcomes.

Probability Mass function is defined for discrete values. For example, a die will always have ${1, 2, 3, 4, 5, 6}$ in the event space. It won’t contain any value like 1.5. Probability Mass Function (PMF) is evaluated at a value corresponding to the probability that a random variable takes that value. It is just a fancy way of describing the same probability theory we discussed above. For a die,

$$P(1) = \frac{1}{6}$$

$$P(2) = \frac{1}{6}$$

$$P(3) = \frac{1}{6}$$

$$P(4) = \frac{1}{6}$$

$$P(5) = \frac{1}{6}$$

$$P(6) = \frac{1}{6}$$

The two probability theorem must be satisfied by a PMF. So,

$$ \sum{P(X)} = \frac{1}{6} +\frac{1}{6} +\frac{1}{6} +\frac{1}{6} +\frac{1}{6} +\frac{1}{6} = 1 $$

and

$$ P(X) >= 0 $$

Probability Density Function (PDF) is the same as PMF, but for a continuous random variable. So for continuous, we will integrate the random variable instead of summing.

$$ \int{P(X)} = 1 $$

Different kinds of Data Distribution

Gaussian Distribution

According to Wikipedia:

In probability theory, a normal (or Gaussian or Gauss or Laplace–Gauss) distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is

$$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$$

In simple words, it is a distribution of data that is centered around a fixed value with no bias in any direction (left or right). The below image is a gaussian distribution. Gaussian distribution is also known as Normal Distribution.

Gaussian distribution has two important properties. The mean of the data, and the variance or standard deviation of the data. In the above image, you can see that mean can change the mode of the data. And standard deviation can change the spreadness or skewness of the data.

Here is the implementation of random Gaussian distribution in python and NumPy:

1
2
3
4
5
6
7
8

import numpy as np

n = 1000
mean = 0.0
variance = 1.0

x = np.arange(n)
fx = np.random.normal(loc=mean, scale=variance, size=n)

Uniform Distribution

When you roll a fair die, the outcomes are 1 to 6. The probabilities of getting these outcomes are equally likely and that is the basis of a uniform distribution. The formula of Uniform distribution is given below, where the range of data $x$ is $[a,b]$.

$$f(x) = \frac{1}{b-a}$$

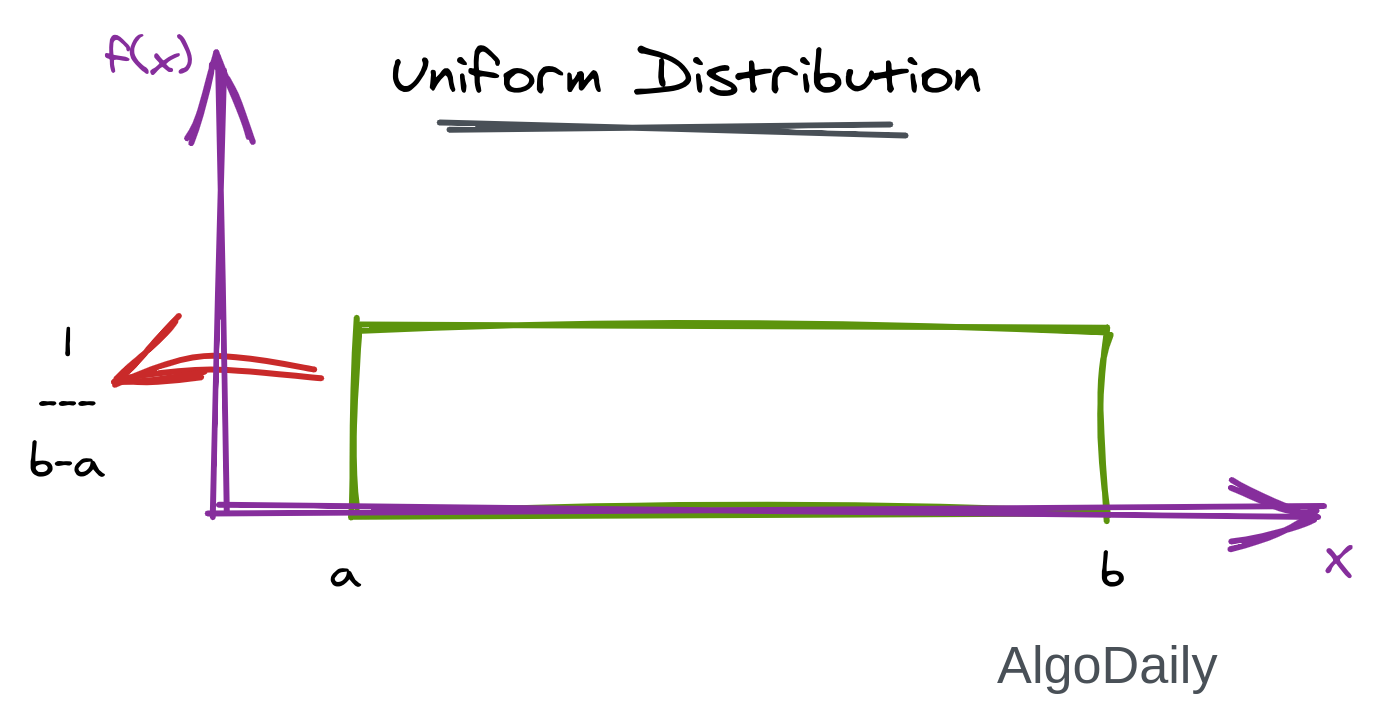
Here is the implementation of random Uniform distribution in python and NumPy:

1
2
3
4
5
6

n = 1000
a = 5.0
b = 10.0

x = np.arange(n)
fx = np.random.uniform(low=a, high=b, size=n)

Poisson Distribution

Poisson Distribution is the closest distribution that represents various events in real life. If you try to model a queueing process in a ticket counter, it will follow a Poisson Distribution. Poisson Distribution is applicable in situations where events occur at random points of time and space wherein our interest lies only in the number of occurrences of the event.

The main conditions of data in Poisson Distribution are:

1. Any event should not influence the outcome of another event.
2. The probability of an event over a short interval must equal the probability of that event over a longer interval.
3. The probability of an event in an interval approaches zero as the interval becomes smaller.

The parameters in Poisson Distribution are $\lambda$ and $t$. Here, $\lambda$ is the rate of an event happening, and $t$ is length of time interval. The formula is as follows:

$$P(x) = e^{-\mu \frac{\mu^x}{x!}}$$

The plot of this distribution is very similar to the plot of normal distribution.

Here is the implementation of random Poisson distribution in python and NumPy:

1
2
3
4
5

n = 1000
interval = 1.0

x = np.arange(n)
fx = np.random.poisson(lam=interval, size=n)

Exponential Distribution

The exponential distribution is widely used for survival analysis. To get an understanding of the expected life of an object, we can use exponential distribution. The formula is as follows:

$$f(x) = \lambda e^{-\lambda x}$$

Here, the parameter $\lambda$ is known as the failure rate of an object at any time $t$, given that it has survived up to time $t$.

So in common sense, an object will survive less if we consider it for a longer time. That is why exponential distribution drops rapidly to zero when x (or $t$) is increased.

Here is the implementation of random Poisson distribution in python and NumPy:

1
2
3
4
5

n = 1000
lamda = 1.0

x = np.arange(n)
fx = np.random.exponential(scale=lamda, size=n)

Statistics on Data Preprocessing

Data normalization

Data normalization is one of the most important steps in data preprocessing (Processing data before any kind of inference). Normalization is a scaling technique in which values are shifted and rescaled so that they end up being inside a range. It is also known as Min-Max scaling.

If we want to normalize a dataset $X$ in the range of [0, 1], we can do this by the following formula.

$$X’ = \frac{X - X_{min}}{X_{max} - X_{min}}$$

If we want the range to be something else, we can do this with a little more tweaking of the above formula.

$$X’ = \frac{X - X_{min}}{X_{max} - X_{min}} * (X_{newmax} - X_{newmin}) + X_{newmin}$$

In python, you can normalize the data X by the snippet below:

1

X_normalized = (X - X.min())/(X.max() - X.min()) * (new_max - new_min) + new_min

Data standardization

Data standardization is another kind of preprocessing very similar to Normalization. Here, the values are centered around the mean with a unit standard deviation. This means that the mean of the attribute becomes zero and the resultant distribution has a unit standard deviation. The formula is:

$$X’ = \frac{X - \mu}{\sigma}$$

Where $\mu$ is the mean of that attribute, and $\sigma$ is the standard deviation of that attribute. We can compute both of them like below:

$$\mu = \frac{\sum_{i=0}^N{X_i}}{N}$$

$$\sigma = \sqrt{\frac{\sum{(x_i - \mu)^2}}{N}}$$

So, where can I use normalization and standardization? Below is a rule of thumb:

1. When the data does not follow a Gaussian distribution, you should use normalization feature scaling. Typically, the K-Nearest neighbor and Neural Network Algorithm need feature scaling.
2. When the data follows a Gaussian distribution, then you should use standardization instead of normalization. Remember, standardization does not have any bounding range. So this might even break your inference model if used inappropriately.

We already did standardize our data in one of our previous lessons. Here is the same code snippet again.

1

X = (X - X.mean(axis=0)) / X.std(axis=0)

Correlation between Variables

In many cases of different machine learning algorithms, you might encounter some highly correlated features. Here, correlated means, one feature can describe another feature very closely. If that is the case, most ML algorithms get biased toward that feature. Also, those duplicate features are extra, meaning they can be removed from the learning process without losing much of the information in the data. Removing highly correlated features fastens the time learning by an algorithm.

A correlation could be positive, meaning both variables move in the same direction, or negative, meaning that when one variable’s value increases, the other variables’ values decrease. As stated earlier, the performance of some algorithms can deteriorate if two or more variables are tightly related. This phenomenon is called multicollinearity.

Correlation between two features can be detected using the Pearson correlation coefficient. The formula is:

$$\rho (X_1,X_2) = \frac{cov(X_1, X_2)}{\sigma_{X_1}\sigma_{X_2}}$$

If $\rho$ is positive and close to 1, the features are highly positively correlated. And if it is close to -1, then they are highly negatively correlated. Otherwise, there is no correlation between the features.

In python, we can calculate correlation between two data as follows:

1
2
3

X_1 = np.array([-2, -1, 0, 1, 2])
X_2 = np.array([4, 1, 3, 2, 0])
my_rho = np.corrcoef(X_1, X_2)

Statistical Hypothesis

Hypothesis testing is a statistical method that is used in making statistical decisions using experimental data. Hypothesis Testing is an assumption that we make about the population parameter.

For example, if you analyze a hospital and try to test whether males are affected more by COVID-19 than women, then it is called hypothesis testing.

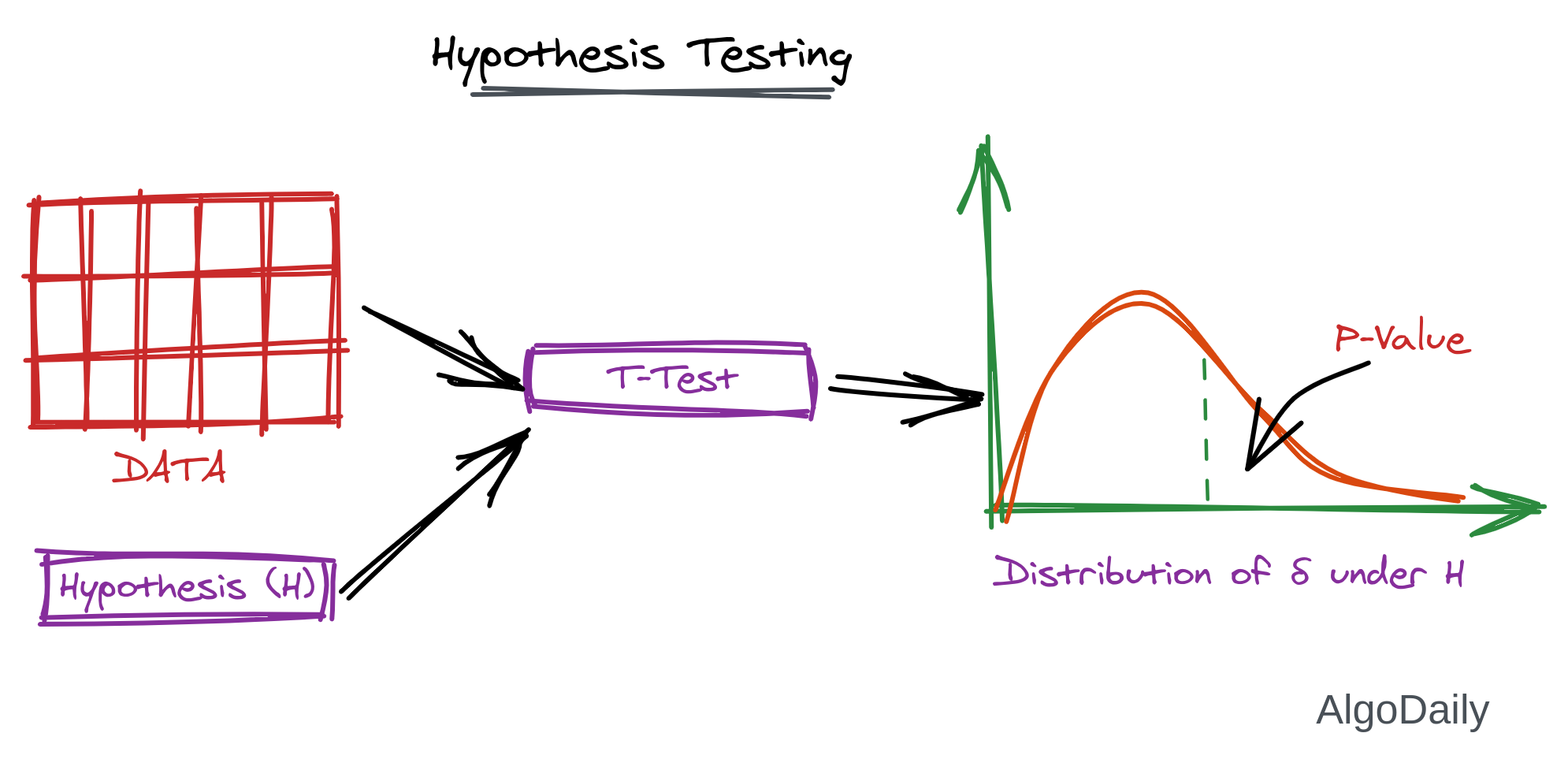
To do this testing, we need to have a hypothesis known as $H_0$ (the null hypothesis). The basic hypothesis is normalization and standard normalization so try to understand these two topics first from above.

The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis. It is usually taken to be that the observations are the result of a real effect (with some amount of chance variation superposed).

After fixing the null and alternative hypothesis, we select a level of significance. The level of significance is how sure you are when you are trying to select a decision.

With a level of significance, we detect a P-Value (calculated probability), probability of finding the observed, or more extreme, results when the null hypothesis ($H_0$) of a study question is true. If we get a very small p-value (0, 0.001, 0.005), we reject the null hypothesis.

Hypothesis testing can be done with different kinds of statistical testing. We will discuss t-test in this lesson. The equation of t-test is given below:

$$t = \frac{\mu_{X_1} - \mu_{X_2}}{\sqrt{\frac{S_{X_1}^2}{n_{X_1} }+ \frac{S_{X_2}^2}{n_{X_2}}}}$$

Where $S$ is the standard deviation of the sample. And $\mu$ is the mean.

We can implement the hypothesis testing easily in Python. But we are going to need a table to compare and get the p-value.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np
from scipy import stats # dont worry about this. We cover it later

N = 10
# Two gaussian distributions
X_1 = np.random.randn(N) + 10 # mu = 10, var = 1
X_2 = np.random.randn(N) + 3 # mu = 3, var = 1

X_1_var = X_1.var(ddof=1)
X_2_var = X_2.var(ddof=1)

S = np.sqrt((var_a + var_b)/2)

# Calculate the t-statistics
t = (X_1.mean() - X_2.mean())/(S*np.sqrt(2/N))

# Now compare the value of t from a t-statistic table to get the p-value. 
## This can be done with a higher-level library scipy. We will learn about this library in a lesson soon.

# Degrees of freedom
df = 2*N - 2
#p-value after comparison with the t 
p = 1 - stats.t.cdf(t,df=df)

# Now that we have a p-value

print(f"t = {t}")
print(f"p = {2*p}")

## Cross Checking with the internal scipy function
t2, p2 = stats.ttest_ind(X_1,X_2)
print(f"t2 = {t2}")
print(f"p2 = {p2}")

Conclusion

In the next lesson, you will get started with beautiful data visualization. In that lesson, we will plot each distribution with some dummy parameters. We can also interact with distributions and understand how they are working.