Leetcode Problem - Four Sum

Problem link: https://leetcode.com/problems/4sum/
Difficulty: Medium
Category: Arrays

Step 1: Grasping the Problem

Given an array of integers, given an array nums and an integer target, we need to find the list of all unique quadruplets that sum to target. It can be easily perceived that we can do a brute force to check all possible combinations in the array resulting in an O(n^4) time complexity solution.

Of course, there is a better solution than O(n^4). Before solving this problem, it is better to get familiar with the famous 2-sum problem. In 2-sum problem, you are given an array and an integer, and you will need to return the pairs of integers which sum to the given integer. The best solution of 2-sum problem is linear in time complexity. YouTube channel Life at Google has a wonderful video on 2-sum problem to have a great intuition.

This problem can be taken as a generalization of 2-sum problem. We can have two loops over the array with first_index and second_index indices and within the loop, we need to find two number that add up to target - nums[first_index] - nums[second_index]. This becomes a reduction to 2-sum problem indeed.

The algorithm must not return duplicate quadruplets. For this reason, while traversing in the array, we need to make sure that no duplicate values are being looped over. The best way to do this is to sort the array first. We have already 2 outer first_index and second_index loops and a linear algorithm within, the worst case will be at least O(n^3). So sorting the array first will help us find duplicate without hurting the complexity of the algorithm.

A general overview with sample input nums = [1, 0, -1, 0, -2, 2] and target = 0 is visualized below. first_index is named i and second_index is named j to save space.

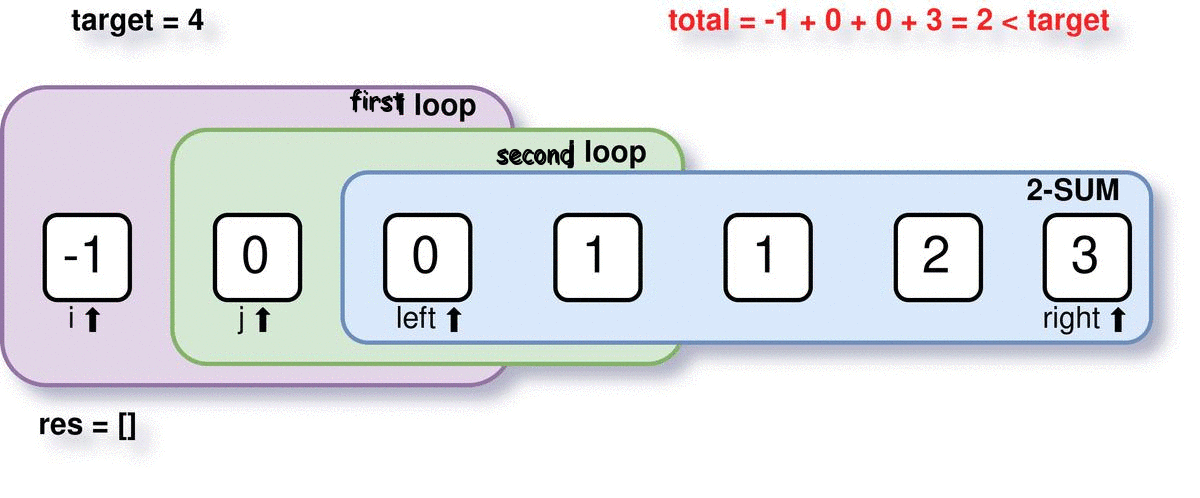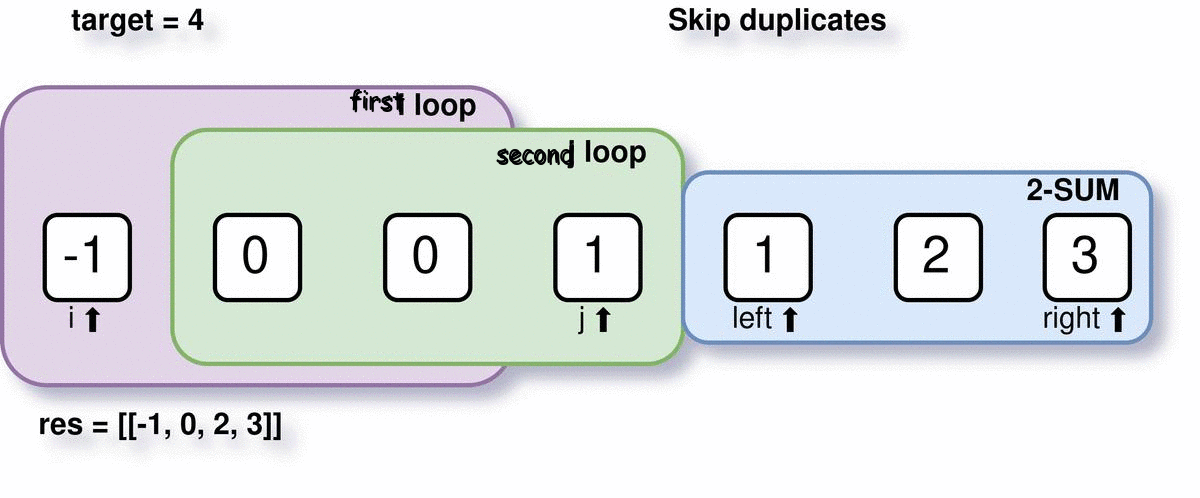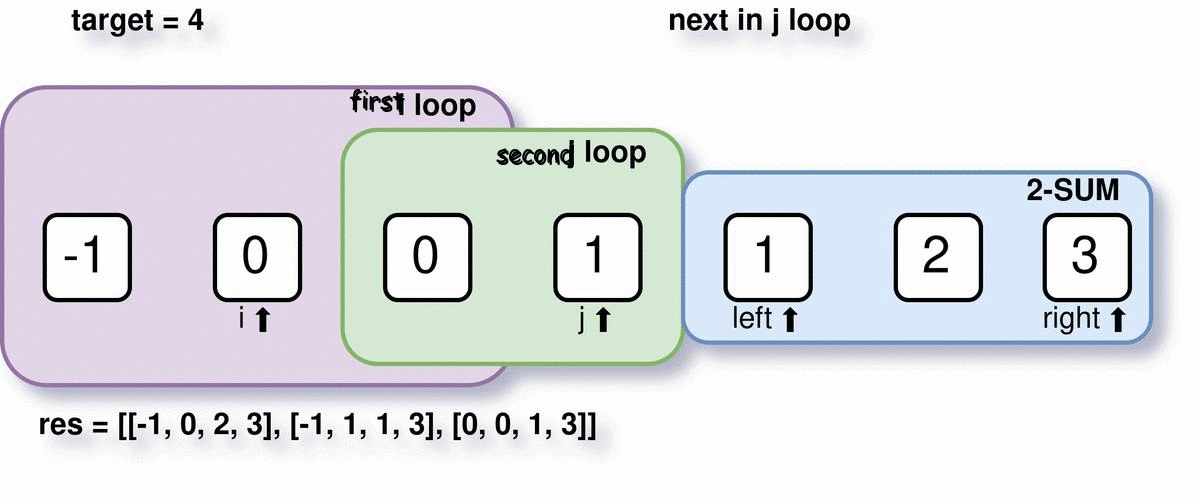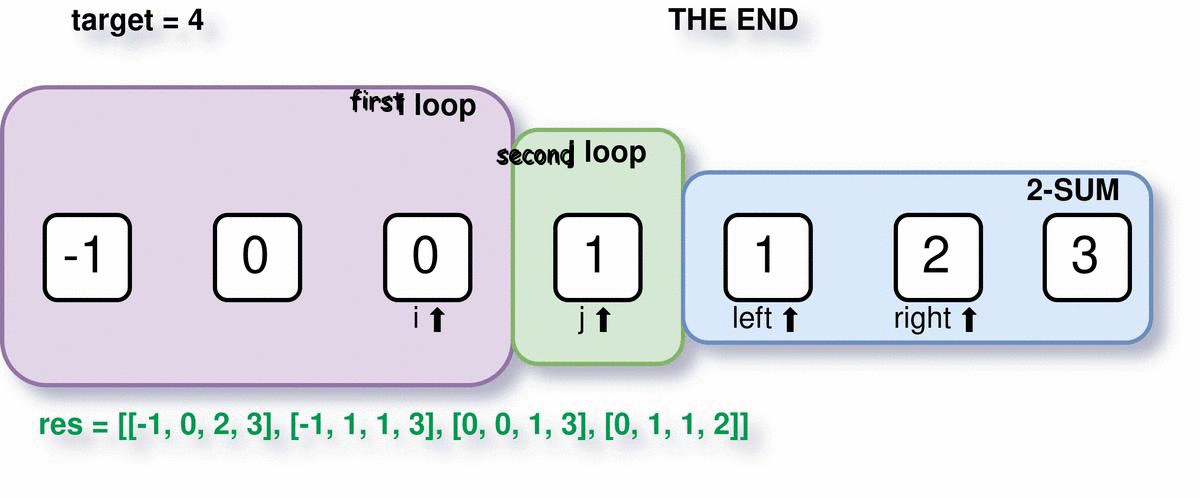
4Sum visualization

Step 2: Initialization and sorting the array

As mentioned earlier, to check duplicates, we will sort the array. We will also create a res array where we are going to store the detected quadruplets.

1
2
nums.sort()
res = []

Step 2: first_index loop

The most outer loop will take care of the first element of the resulting quadruplets. We will run this loop from the first element of the array till the last possible element we can include as the first item in resulting quadruplets. As quadruplets has 4 elements, there should be at least 3 elements left in the array for the first_index loop.

1
2
# first loop till third last number
for first_index in range(len(nums)-3):

Step 3: Skip duplicate first element

As the array is now sorted, all equal elements will be neighboring. So after the first iteration of first_index loop, if we again encounter the same element, we need to skip that to avoid duplicates. So we need to check if we are in the first iteration, and if we already have seen this element or not.

1
2
    if first_index > 0 and nums[first_index] == nums[first_index-1]:
        continue

Step 4: second_index loop

The second_index loop is very much similar to the first_index loop. We will start from the next element of first_index, and end leaving 2 elements in the array. In this step, we will also skip the duplicates for the second element of quadruplets.

1
2
3
4
    # Second loop till second last number
    for second_index in range(first_index+1, len(nums)-2):
        if second_index>first_index+1 and nums[second_index] == nums[second_index-1]:
            continue

Step 5: 2-SUM

The first two elements of the quadruplets have been taken care of. Now we just need to solve a 2SUM problem from (second_index+1)th element to the last element. There are many ways to solve this problem. Usually hashset is used to keep track of the seen elements and search in the rest of the array for a complement to sum element. But this is used because the array is not sorted. Using a hashset leads to O(n) space complexity for 2-sum problem. If the array is already sorted, we can use two-pointer shrinking method to solve 2-sum problem.

In two pointer shrinking method, we start with two variables left and right being on two ends of the remaining array. Then we check if we got the desired sum or not. If total value of quadruplet is greater than target, we need a smaller sum, so we move pointer right one index left. If total is smaller than target, we need a bigger sum, so we move pointer left one index right. This process is continued until the pointers overlap each other (or the window is shrank to zero). Finally, if total == target, we have a quadruplet! Simply add it to res. This time, we shrink the window from both sides to keep total as unchanged as possible.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
# Two sum problem
left = second_index+1
right = len(nums) - 1
while left < right:
    sample = [nums[first_index] + nums[second_index] + nums[left] + nums[right]]
    
    total = sum(sample)
    if total < target:
        left += 1
    elif total > target:
        right -= 1
    else:
        res.append(sample)
        left += 1
        right -= 1

But this will not be sufficient to solve the problem because we have not yet taken care of duplicates inside the 2-sum window. To do this, while shrinking the window, we see if the value we are getting in left or right is already found or not. This is not necessary if total != target because it will eventually be automatically skipped in the next iteration in while (total will not change, so total != target remains False).

1
2
3
4
5
6
7
        left += 1
        while nums[left] == nums[left-1] and left < right:
            left += 1

        right -= 1
        while nums[right] == nums[right+1] and left < right:
            right -= 1

Step 5: Return result

After all the loops are finished, we can simply return the res variable we have been using to log quadruplets.

1
return res

Step 6: Handle Corner Cases

This problem will work for all natural numbers (will work also for floating points). Also we do not need to check for undersized nums because the first_index loop will never run if len(nums) < 4.

Finally the algorithm takes O(n*n*n) time complexity and O(1) space complexity. This can not be further optimized because there is a proof for 3-sum (similar to 2-sum and 4-sum) problem to take at least O(n^3) time. The complete program is given below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution:
    def fourSum(self, nums: [int], target: int) -> [[int]]:
        # Handle corner case
        if len(nums) < 4:
            return []

        nums.sort()
        res = []

        # first loop till third last number
        for first_index in range(len(nums)-3):
            # Skip duplicates
            if first_index > 0 and nums[first_index] == nums[first_index-1]:
                continue

            # Second loop till second last number
            for second_index in range(first_index+1, len(nums)-2):
                # Skip duplicates
                if second_index>first_index+1 and nums[second_index] == nums[second_index-1]:
                    continue

                # Two sum problem
                left = second_index+1
                right = len(nums) - 1
                while left < right:
                    sample = [nums[first_index], nums[second_index], nums[left], nums[right]]
                    total = sum(sample)

                    # move left boundary
                    if total < target:
                        left += 1
                    # move right boundary
                    elif total > target:
                        right -= 1

                    # found match!
                    else:
                        res.append(sample)

                        # move left next until new value found
                        left += 1
                        while nums[left] == nums[left-1] and left < right:
                            left += 1

                        # move right next until new value found
                        right -= 1
                        while nums[right] == nums[right+1] and left < right:
                            right -= 1
        return res

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        // Handle corner case
        if(nums.size() < 4)
            return {};

        sort(nums.begin(), nums.end());
        vector<vector<int> > res;

        // first loop till third last number
        for(int firstIndex = 0; firstIndex < nums.size() - 3; firstIndex++) {
            // Skip duplicates
            if(firstIndex > 0 && nums[firstIndex] == nums[firstIndex-1])
                continue;

            // Second loop till second last number
            for(int secondIndex = firstIndex+1; secondIndex < nums.size() - 2; secondIndex++) {
                // Skip duplicates
                if(secondIndex > firstIndex + 1 && nums[secondIndex] == nums[secondIndex - 1])
                    continue;

                int left = secondIndex + 1;
                int right = nums.size() - 1;
                while(left < right) {
                    vector<int> sample = {
                        nums[firstIndex],
                        nums[secondIndex],
                        nums[left],
                        nums[right]
                    };

                    int total = accumulate(sample.begin(), sample.end(), 0);
                    
                    // move left boundary
                    if(total < target)
                        left++;
                    // move right boundary
                    else if(total > target)
                        right--;
                    
                    // found match!
                    else {
                        res.push_back(sample);
                        left++;
                        while(nums[left] == nums[left-1] && left < right)
                            left++;
                        right--;
                        while(nums[right] == nums[right+1] && left < right)
                            right--;
                    }
                }
            }
        }
        return res;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        // Handle corner case
        if(nums.length < 4)
            return new ArrayList<>();

        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();

        // first loop till third last number
        for(int firstIndex = 0; firstIndex < nums.length-3; firstIndex++) {
            // Skip duplicates
            if(firstIndex > 0 && nums[firstIndex] == nums[firstIndex - 1])
                continue;

            // Second loop till second last number
            for(int secondIndex = firstIndex+1; secondIndex < nums.length - 2; secondIndex++) {
                // Skip duplicates
                if(secondIndex > firstIndex + 1 && nums[secondIndex] == nums[secondIndex - 1])
                    continue;

                int left = secondIndex + 1;
                int right = nums.length - 1;
                while(left < right) {
                    List<Integer> sample = new ArrayList<>(
                        Arrays.asList(
                            nums[firstIndex],
                            nums[secondIndex],
                            nums[left],
                            nums[right]
                        )
                    );

                    int total = 0;
                    for(int num: sample)
                        total += num;
                    
                    // move left boundary
                    if(total < target)
                        left++;
                    // move right boundary
                    else if(total > target)
                        right--;
                    
                    // found match!
                    else {
                        res.add(sample);
                        left++;
                        while(nums[left] == nums[left-1] && left < right)
                            left++;
                        right--;
                        while(nums[right] == nums[right+1] && left < right)
                            right--;
                    }
                }
            }
        }
        return res;
    }
}