Step 1: Grasping the Problem

You are given a list of airline tickets in [from, to] format and you will need to construct an itinerary in order starting from a fixed airport "JFK". The key points to mention in this question are:

• Lexical ordered itinerary should be constructed if there are multiple itinerary possible.
• It is guaranteed that an itinerary with using all tickets is possible.
• One must use all the tickets and start from "JFK".

Because there are a lot of visiting and traversal going on, one can surely tell that this is a graph theory problem. So first and foremost thing to do is create a graph from the given tickets.

In the graph, the airports will be nodes and the tickets will be edges. According to the problem stated above, we can say “using all tickets exactly once” means “using all edges exactly once” in the graph. So in this graph problem, one needs to use all edges no matter if you visit the nodes or not. Hearing this, if you are familiar, you will say this is the application of Eulerian Path Construction Algorithm.

There are a lot of algorithms to construct the eulerian path from both directed and undirected graphs e.g. Fleury’s algorithm, Hierholzer’s algorithm etc. Our graph is directed and we will construct the path with a modified version of Hierholzer’s algorithm.

Step 2: Reverse sort the tickets

Because we need the first lexicographic ordered solution, we need to traverse the graph is lexicographic order. For this, we will construct the graph in a way so that the adjacency list’s descendants will be ordered. For this, we will sort the tickets in descending order.

1
2

# To maintain the lexical order
tickets.sort(reverse=True)

Step 2: Build the Graph

The first part of solving a graph theory problem has always been constructing the graph itself. In python it is now-a-days usual to represent a graph with dictionary graph where the keys are sources and values are list of descendants of each edge. This is an adjacency list representation of the graph.

Many use defaultdict to create the graph, but to keep things simple, we will use “default” dict of python instead. Just loop through the edges (tickets in this problem) and append a src dst to the graph dict.

1
2
3
4
5
6

# Build the graph
graph = {}
for src, dst in tickets:
    if src not in graph:
        graph[src] = []
    graph[src].append(dst)

Step 3: Eulerian Path Construction

A graph may or may not have eulerian paths depending on where the edges it has. Hierholzer’s algorithm first checks if the graph has a feasible Eulerian path in it. To check that, it follows the following table.

There are four flavors of Euler path/circuit problem we care about:

This problem guarantees that there must be at least one eulerian path in it. So we do not need to check whether there is one or not.

After detecting the existence of Eulerian path, the algorithm does the two things:

1. Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph.
2. As long as there exists a vertex u that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u, and join the tour formed in this way to the previous tour.
3. Since we assume the original graph is connected, repeating the previous step will exhaust all edges of the graph.

So we can use a list named route to keep track of “joining the tour formed in this way”. We can also create and call a recursive function to do “repeating the previous step” to “exhaust all edges” and get the final route in backward.

A demonstration of the algorithm is given below. Note that, this graph does not have a valid itinerary to use all tickets, still the algorithm takes as much tickets as possible and build an itinerary.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

# Eulerian path
route = []
def visit(airport):
    # DFS-like visiting all node
    while airport in graph and graph[airport]:
        dst = graph[airport].pop()
        visit(dst)
    # push the first non-visited node
    route.append(airport)
visit('JFK')

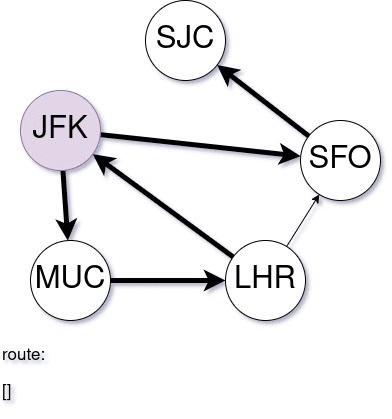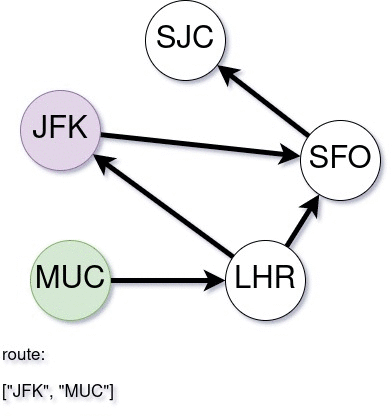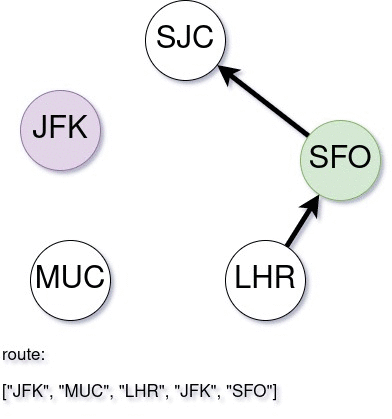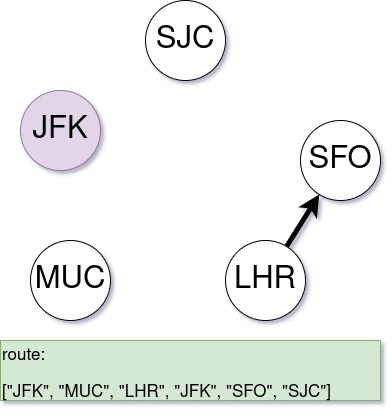
Step 4: Reverse and Return route

Finally, we have route with the eulerian path in backward direction. So we will reverse the path and return it as a result.

1
2

# Return in reverse
return reversed(route)

The time complexity of this problem is O(ELogE) where E is the number of edges (tickets), and V is the number of nodes (airports). The space complexity is order of O(E) because we are just storing the graph with a dict. The small but efficient full code is given below:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution:
    def findItinerary(self, tickets: [[str]]) -> [str]:
        # To maintain the lexical order
        tickets.sort(reverse=True)

        # Build the graph
        graph = {}
        for src, dst in tickets:
            if src not in graph:
                graph[src] = []
            graph[src].append(dst)

        # Eulerian path
        route = []
        def visit(airport):
            # DFS-like visiting all node
            while airport in graph and graph[airport]:
                dst = graph[airport].pop()
                visit(dst)
            # push the first non-visited node
            route.append(airport)
        visit('JFK')

        # Return in reverse
        return reversed(route)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

class Solution {
    unordered_map<string, vector<string> > graph;
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        // To maintain the lexical order
        sort(tickets.begin(), tickets.end(), [] (vector<string> &first, vector<string> &second) -> bool {
            bool tmp = lexicographical_compare(first[0].begin(), first[0].end(), second[0].begin(), second[0].end());
            if(first[0] == second[0])
                return lexicographical_compare(first[1].begin(), first[1].end(), second[1].begin(), second[1].end());
            return tmp;
        });
        reverse(tickets.begin(), tickets.end());

        // Build the graph
        for(auto ticket: tickets)
            graph[ticket[0]].push_back(ticket[1]);
        
        // Eulerian path
        vector<string> route;
        visit("JFK", route);

        // Return in reverse
        reverse(route.begin(), route.end());
        return route;
    }

private:
    void visit(string airport, vector<string> &route) {
        // DFS-like visiting all node
        while(graph.find(airport) != graph.end() && graph[airport].size() != 0) {
            auto dst = graph[airport].back();
            graph[airport].pop_back();
            visit(dst, route);
        }
        // push the first non-visited node
        route.push_back(airport);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
    Map<String, PriorityQueue<String>> graph;

    public List<String> findItinerary(List<List<String>> tickets) {
        // Unlike python, where we manually sorted tickets.
        // We will use map with PriorityQueue as value which is faster

        // Build the graph
        graph = new HashMap<>();
        for (List<String> ticket : tickets) {
            graph.putIfAbsent(ticket.get(0), new PriorityQueue<>());
            graph.get(ticket.get(0)).add(ticket.get(1));
        }

        // Eulerian path
        LinkedList<String> route = new LinkedList<>();
        visit("JFK", route);

        return route;
    }

    private void visit(String airport, LinkedList<String> route) {
        PriorityQueue<String> priorityQueue = graph.get(airport);
        // DFS-like visiting all node
        while(priorityQueue != null && !priorityQueue.isEmpty())
            visit(priorityQueue.poll(), route);
        route.addFirst(airport);
    }
}