3D Reconstruction with MPSE

The following images are interactive!!!

All of the experiments done for this research are managed by neptune.ai which can be found in this link.

Multi-Perspective Simultaneous Embedding with MDS

A single page quick review of this paper can be found here.

MPSE stands for Multi-Perspective Simultaneous Embedding which is a method proposed by Dr. Stephen Kobourov et. al. for visualizing high-dimensional data, based on multiple pairwise distances between the data points. Specifically, MPSE computes positions for the points in 3D and provides different views into the data by means of 2D projections (planes) that preserve each of the given distance matrices. There are two versions of it: fixed projections and variable projections. MPSE with fixed projections takes as input a set of pairwise distance matrices defined on the data points, along with the same number of projections and embeds the points in 3D so that the pairwise distances are preserved in the given projections. MPSE with variable projections takes as input a set of pairwise distance matrices and embeds the points in 3D while also computing the appropriate projections that preserve the pairwise distances. The proposed approach can be useful in multiple scenarios: from creating simultaneous embedding of multiple graphs on the same set of vertices, to reconstructing a 3D object from multiple 2D snapshots, to analyzing data from multiple points of view.

Using this point embedding algorithm, we have decided to use it for 3D model reconstruction from multiple 2D images. So we propose a novel algorithm to embed image keypoints in a 3D image. The problem assumes a set of image keypoints in an unknown 3D image and several snapshots (2D pictures) of this scene containing these keypoints, either partially of possibly all of the points. Given the coordinates of these keypoints in each snapshot the problem asks to recover their positions in the original 3D image such that the corresponding projections.

There are a lot of 3D reconstruction methods, especially in the field of computer vision with deep learning. But our proposal stands novel and benificial over many ways than deep learning which keep it’s use-case separate from those of deep learning applications. We do not need any supervised training or any pre-existing dataset. As a result, we also do not have the risks that come with deep learning, like overfitting, high training time or data acquisition phase complexity.

3D Reconstruction with MPSE

3D reconstruction using MPSE would have been a straight forward application problem if the perspective images were ideal, e.g. all the points of a single object can be visible in all the images. But it is impossible for all the sides or points of an object to be visible from all the sides. So we had to come up with modifications to the original MPSE algorithm to come up with hidden points (points that are visible from at least 1 viewpoint but not all viewpoints).

Assume we have in total $N$ keypoints that we aim to embed in 3D. However, each of the given view for $1 \le k \le K$ does not include all of these $N$ points. We assume we are given parameters $\alpha_i^k$ for $1 \le k \le K$ and $1 \le i \le N$ which is 1 if the $i$-th points is visible in $k$-th view and 0 otherwise. we can alternatively introduce variables $\alpha_{ij}^k$ which would have a value $1$ if both $i$-th and $j$-th keypoints are visible in $k$-th view and 0 otherwise. The modified objective function for MPSE would be as follows
% The objective function for MPSE with possible hidden points:
\begin{equation}
\sum_{k = 1}^K \sum_{i > j} \alpha^k_{ij} \left( D^k_{i j} - \Vert P^k(x_i) - P^k(x_j) \Vert \right)^2.
\end{equation}
Where $\alpha^k_{ij}$ is either $1$ or $0$. It is 1 when both points $i$ and $j$ are present in projection $k$ otherwise it is 0.
Similarly, if with the use of $\alpha_i^k$, the objective dunctiuon would have the following form:
\begin{equation}
\label{eq:MPSE_hidden_points}
\sum_{k = 1}^K \sum_{i > j} \alpha^k_{i} \alpha^k_{j} \left( D^k_{i j} - \Vert P^k(x_i) - P^k(x_j) \Vert \right)^2.
\end{equation}
where $\alpha^k_{i} = 1$ if the $i$-th point is present and set $\alpha^k_{i} = 0$ if the point is missing.

Our overall contribution in this is shown in the image at the top of this page. Some of the 3D pointsclouds that were reconstructed from only 3 images taken from different positions is given below:

Dataset Requirements

The exact dataset that MPSE needs should have the following features:

A set of perspectives of a pointcloud. A perspective is a set of points of a specific pointcloud transformed or projected onto n-dimension. The goal is to reconstruct the pointcloud in m-dimension where $n < m$.
An annotation of correspondence of each point in different perspectives.

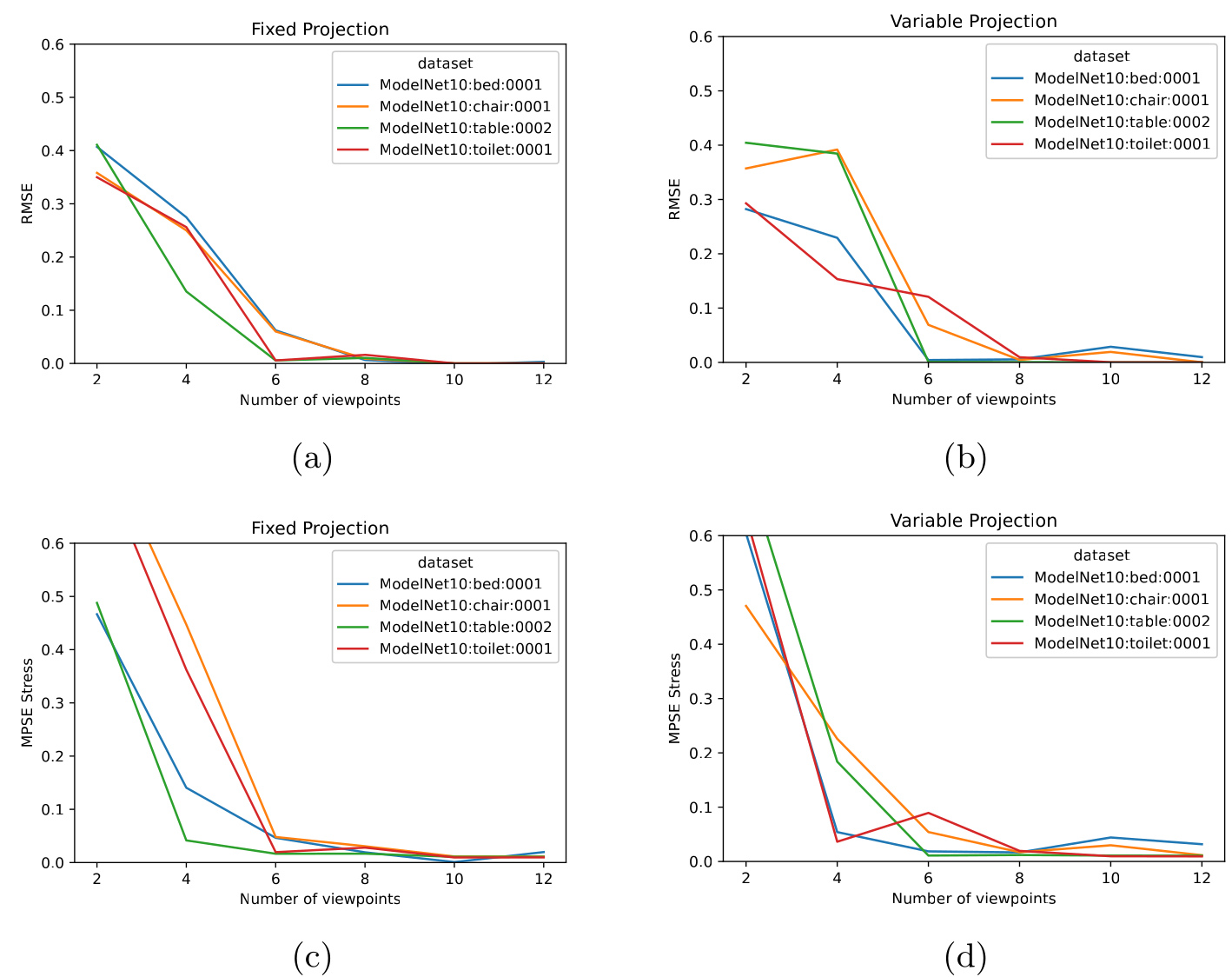
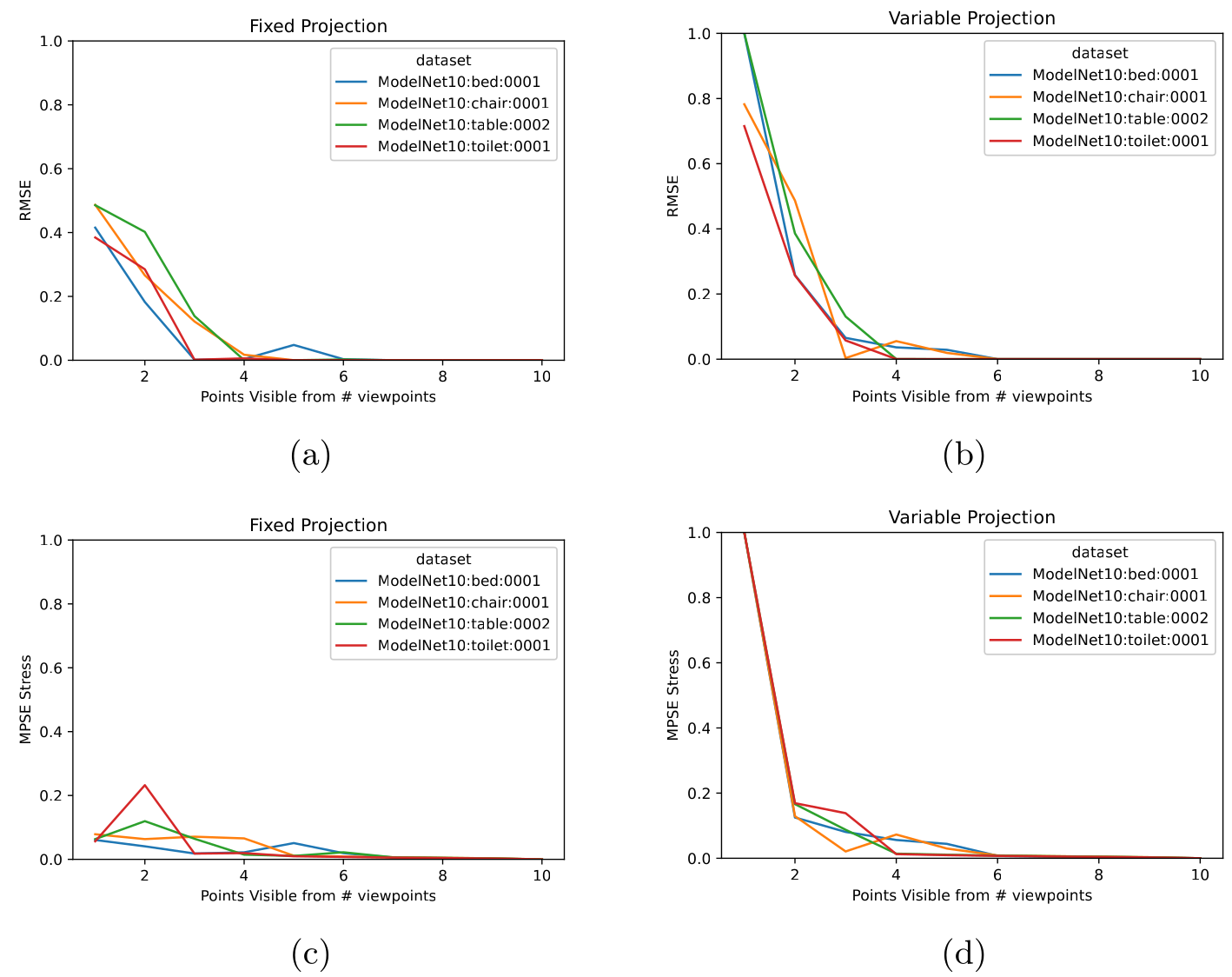
Evaluation

The evaluation of the MPSE algorithm is done based on different parameters of the model and the dataset.

The dissimilarity of two pointcloud is calculated using equation the below equation. Here $x_i$ is the $i$th point of newly generated point cloud and $y_i$ is $i$th point of the ground truth pointcloud.

$$\mathcal{L}(x, y) = \frac{\sum{||x_i - y_i||_2}}{n}$$

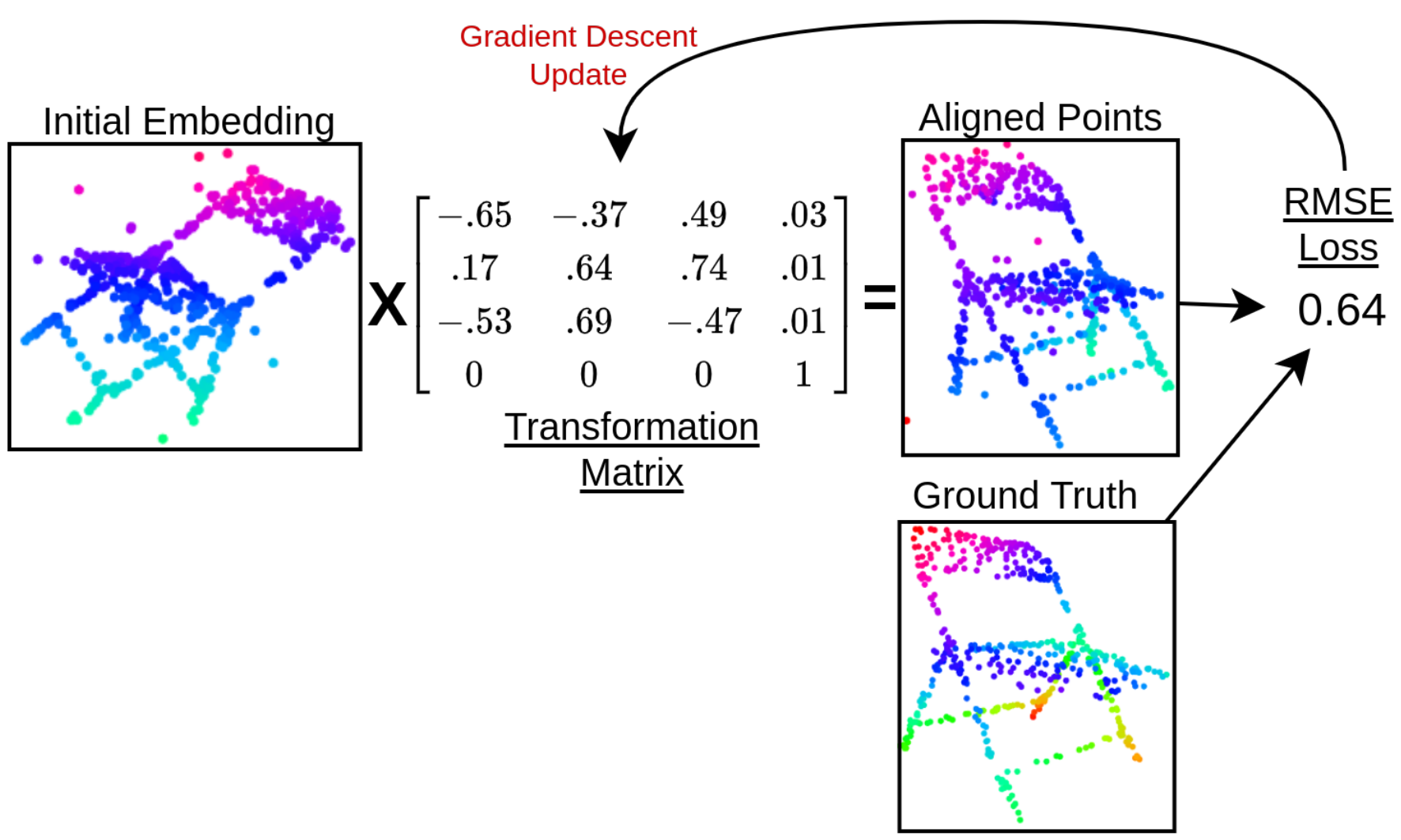
The loss function which is optimize For alignment of two pointclouds before calculating the distance is given

\begin{equation}
min_{T}\mathcal{L}(T.x, y)
\end{equation}

Here, $T$ is a 4*4 function and $x$ is the vector of generated point cloud in homogeneous coordinates. $y$ is also of the same form.

After having trails of different optimization functions, we found Adam optimizer to converge the fastest. The whole points alignment algorithm is expressed in the following figure: