Step 1: Grasping the Problem

We need to get the length of the maximum substring from a given string where the substring must not have any duplicate characters. We do not need to return the substring. So we do not need to care about the order of the substrings.

As we do not need the string, we just need to take care of the frequencies of the largest string. In a more “targeting towards the solution” way, we need to keep the characters of largest string so far stored so that when we try to make the string larger by concatenating more characters, we can make sure that it is not already in the stored characters. Hashset is a perfect data-structure for the following use. Python has built in set for this.

Also, a substring is a sequential subset of the given string string. And we need to expand this sequential subset as large as possible. This tells us that a sliding window maximization approach is best to solve this problem.

In a sliding window maximization problem, we start from the first element with window size one. Then we try to expand the window by one-by-one element until we can’t. Then we shrink the window until again we become able to increase it. Everytime we increase, we could track both the largest substring and it’s length. Below is a small demonstration of what a sliding window approach would look like.

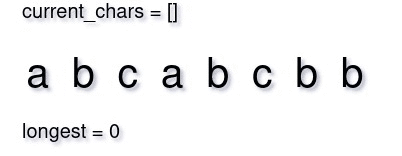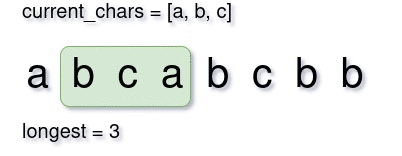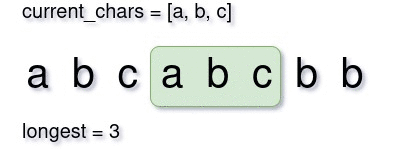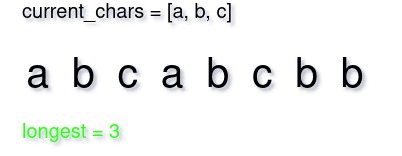
Step 2: Sliding Window Initialization

A sliding window needs four things to operate.

1. The left boundary of the window (left for this solution).
2. The right boundary of the window (right for this solution).
3. The target variable (longest for this solution). This variable stores the target we want to get from the window. It can be many variables or states like the starting and ending of the substring. But in this solution, we only need the length of the largest substring.
4. Any intermediate variables to assert the conditions of window expanding/shrinking ability. In this problem, it is current_chars which stores the characters of the largest string.

So the initialization will look something like this:

1
2
3

longest = 0             # Answer
left, right = 0, 0      # Window bounds
current_chars = set()   # Chars within current window

Step 3: Loop for the window

The sliding window will run until we have reached the end of the string. But do we need the left variable to reach the end too? No, because we need only the largest value. Moving left towards end will only shrink the window making longest smaller that it is now.

So looping until right has reached end will suffice.

1

while right < len(string):

Step 4: Expand the window

We can only expand the window when the new character is not in current_chars list. After checking if we can add the character, we need to add that character to current_chars to check for new characters in the future.

We also need to increase longest if it becomes larger than the previous one. And finally we need to expand the window boundary to one character right.

1
2
3
4
5

# Expand window
if string[right] not in current_chars:
    current_chars.add(string[right])
    right += 1
    longest = max(longest, right - left)

Step 5: Shrink the window

If we cannot expand the window, we will need to shrink it. We will shrink it until the new character is removed from current_chars. This can be taken care by the while loop we created earlier. And after removing the leftmost character of the window, we will move the left boundary of the window one character right.

1
2
3
4

# Shrink window
else:
    current_chars.remove(string[left])
    left += 1

Step 6: Return longest

After the while loop ends, we will surely get the longest substrings length. We will return it after the while loop.

1

return longest

Every sliding window problem takes O(n) time itself, where n is the length of the string. Inside the loop, we are making a look-up in a hashset and incrementing and decrementing variable. All these take O(1) time. So the time complexity of the algorithm is O(n) and space complexity is also O(n) in the worst case. The program is given below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution:
    def lengthOfLongestSubstring(self, string: str) -> int:
        longest = 0             # Answer
        left, right = 0, 0      # Window bounds
        current_chars = set()   # Chars within current window
        while right < len(string):
            # Expand window
            if string[right] not in current_chars:
                current_chars.add(string[right])
                right += 1
                longest = max(longest, right - left)
            # Shrink window
            else:
                current_chars.remove(string[left])
                left += 1
        return longest

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    int lengthOfLongestSubstring(string str) {
        int longest = 0;            // Answer
        int left = 0, right = 0;    // Window bounds

        // Chars within current window
        set<char> currentChars;
        while(right < str.length()) {
            // Expant window
            if(currentChars.find(str[right]) == currentChars.end()) {
                currentChars.insert(str[right++]);
                longest = max(longest, right - left);
            }
            // Shrink window
            else {
                currentChars.erase(str[left++]);
            }
        }
        return longest;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
    public int lengthOfLongestSubstring(String string) {
        int longest = 0;            // Answer
        int left = 0, right = 0;    // Window bounds

        // Chars within current window
        Set<Character> currentChars = new HashSet<>();
        while(right < string.length()) {
            // Expand window
            if(!currentChars.contains(string.charAt(right))) {
                currentChars.add(string.charAt(right));
                right++;
                longest = Math.max(longest, right - left);
            }
            // Shrink window
            else {
                currentChars.remove(string.charAt(left));
                left++;
            }
        }
        return longest;
    }
}