Step 1: Grasping the Problem

Many people classify this popular “Minimum number of jumps” problem into a dynamic programming problem. In spite of it being truely a dynamic programming problem, it can be solved without noticing any dynamic programming behavior in it. The problem will give you a non-negative integer array nums, where each element defines the maximum length of jump one can make from that index. Starting from index 0, you need to determine the minimum number of jumps required to reach the end of the array.

Below are some important inference one might miss from this problem.

• Although the problem does not say anything whether you can jump backward or not, it is not necessary because each element of the array represents maximum jump length. That means of course, you can make shorter jumps in order to get the best result.
• From an element, the farthest point we can go will never decrease for the forthcoming elements. So if we are at ith stair and the farthest stair we could go is farthest_possible, farthest_possible will always increase for i+k where k is |nums|-i.
• We do not need the last value of nums. Because we will never jump from the last index (it is the destination).

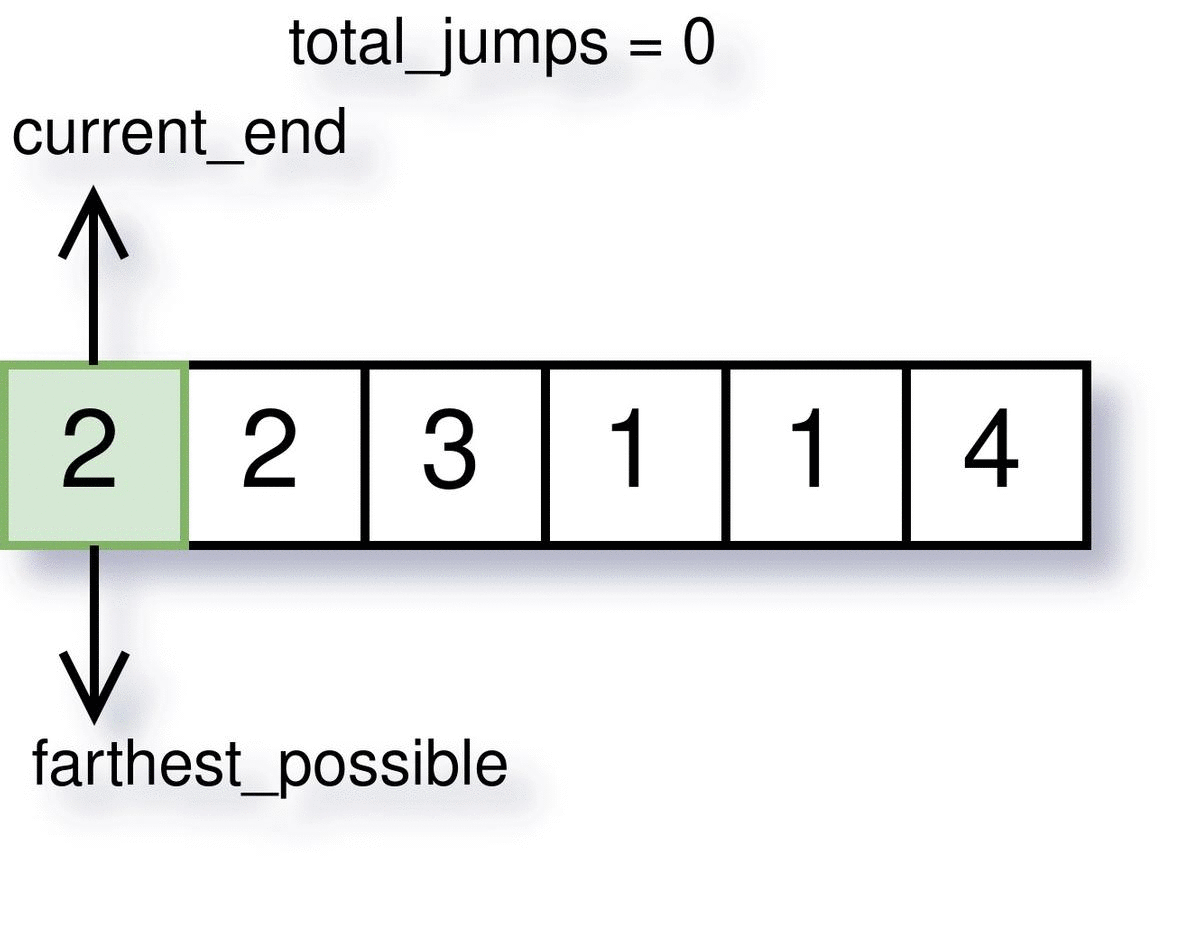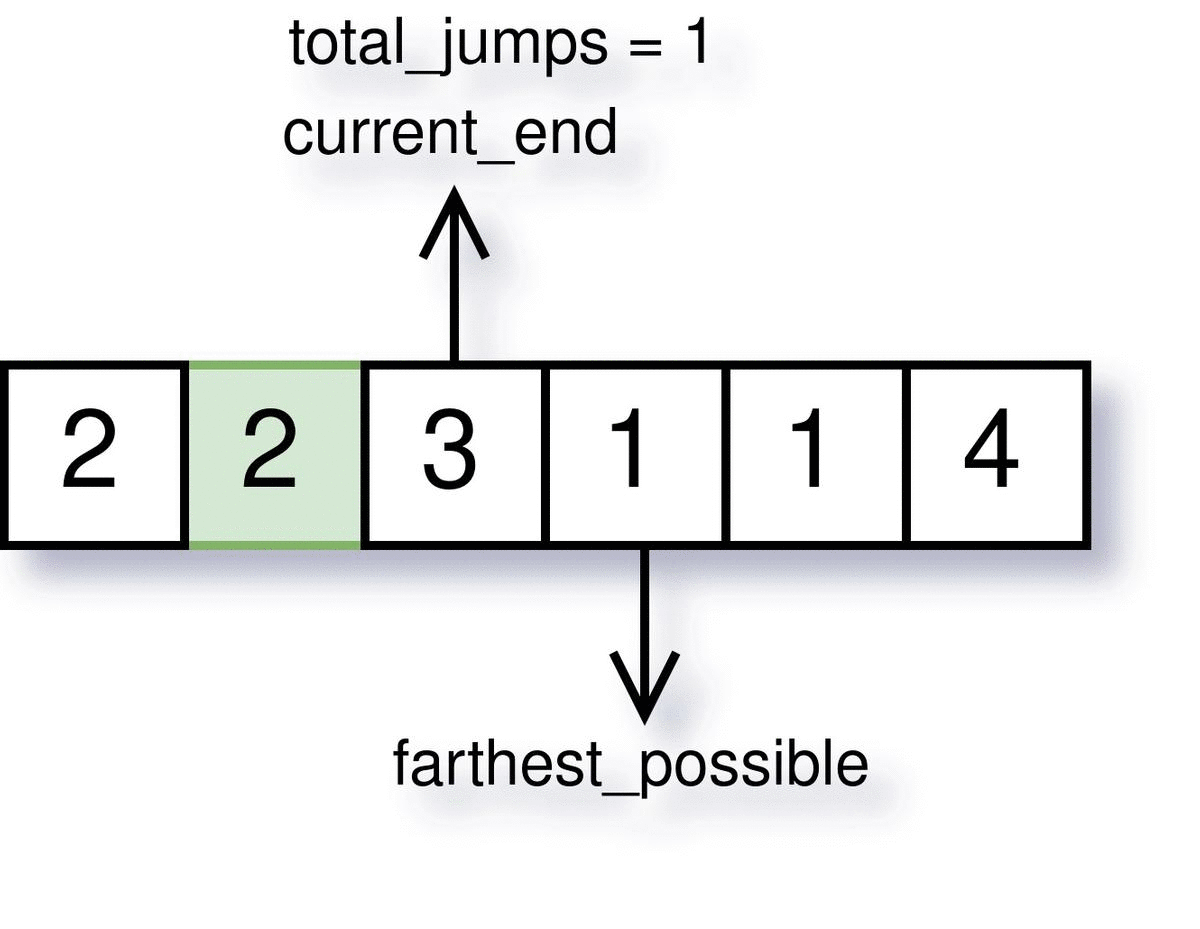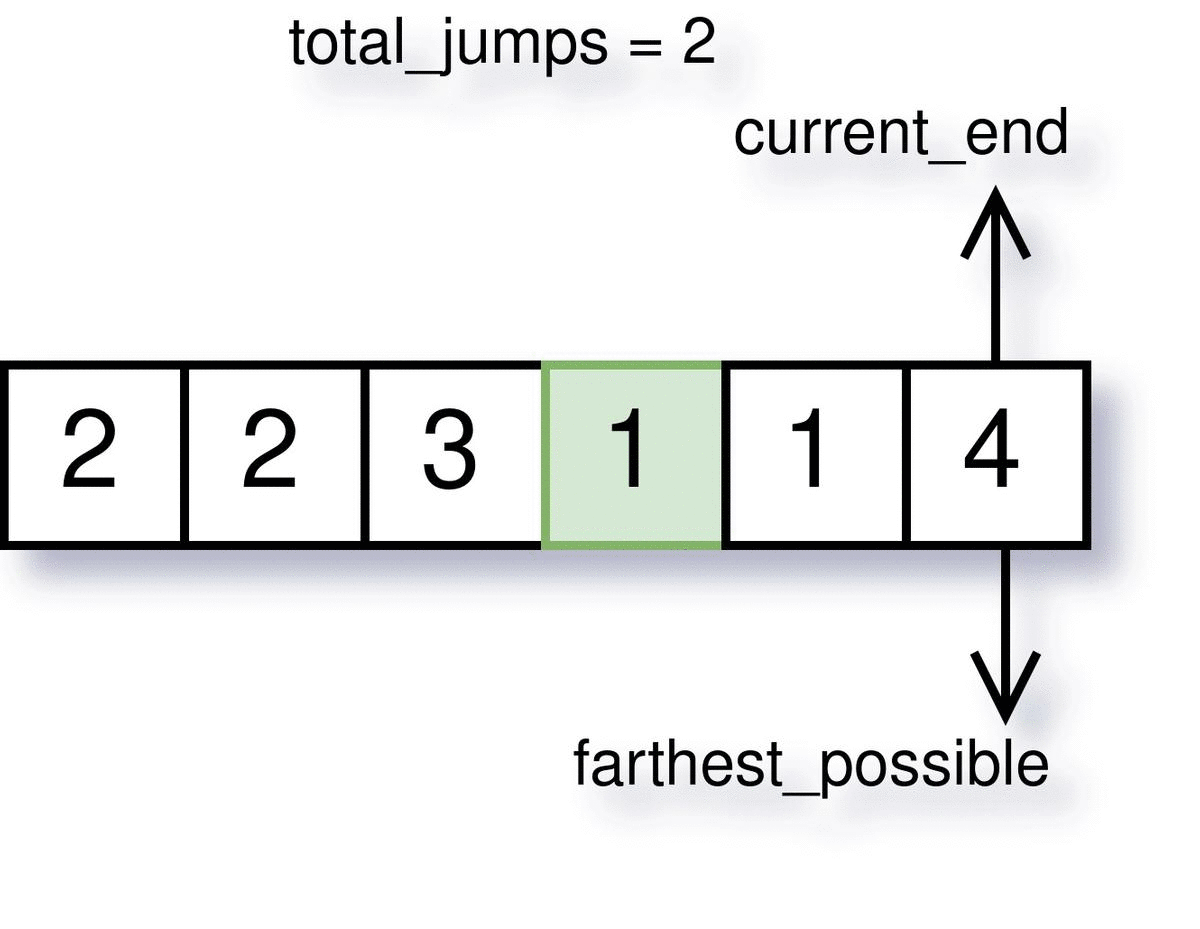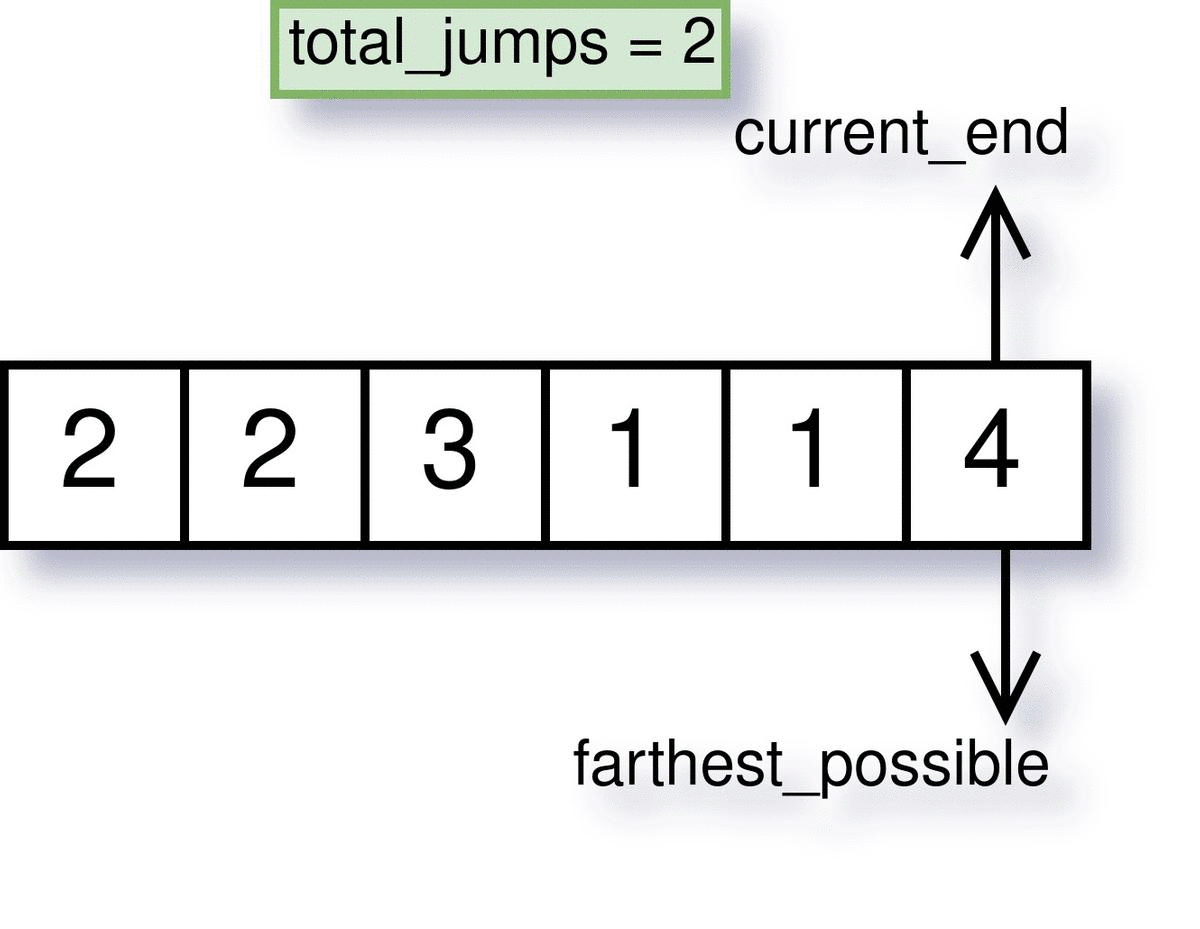
Step 2: Keep track of farthest stair possible

We can start iterating through nums and keep track of the farthest stair we can go from any previous index. For index i, it will be max(k + nums[k]) where k = 0:i. We will also initialize a variable names total_jumps to store the result. Notice how we are leaving the last index of the array in the loop.

1
2
3
4
5
6

total_jumps = 0
current_end = 0         # We will use this on step 3
farthest_possible = 0   # Or any negative value
for jump_ind, jump_len in enumerate(nums[:-1]):
    # Update farthest index I can reach
    farthest_possible = max(farthest_possible, jump_ind + jump_len)

Step 3: Keep track of last jump end

When we reach at a stair which is farthest from the last jump we made, we need to make a new jump. And this jump is not necessarily needed to make from the current index. We can make a jump from any stair before (preferably from that stair which will send us to the farthest_possible).

But as soon as we make a jump, we need to keep track of the farthest jump during that time (let this stored variable be current_end). Next time at each index, we will check if we have reached the end of the last jump or not.

1
2
3
4

# We have to use a new jump from any previous stair and reach farthest
if jump_ind == current_end:
    total_jumps += 1
    current_end = farthest_possible

The visualization of how farthest_possible, current_end and total_jumps work is demonstrated below.

Step 4: Return the total jumps

After the iteration ends, total_jumps will hold the total jumps needed to reach the last index.

1

return total_jumps

We are assuming that it is guaranteed to reach the end of the array. But it is pretty easy to handle, just check if farthest_possible is less than jump_ind.

This algorithm runs only a single loop, so it takes O(n) time and O(1) space complexity. The complete program is given below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def minJump(self, nums: [int]) -> int:
        total_jumps = 0
        current_end = 0
        farthest_possible = 0

        for jump_ind, jump_len in enumerate(nums[:-1]):
            # Update farthest index I can reach
            farthest_possible = max(farthest_possible, jump_ind + jump_len)
            # We have to use a new jump from any previous stair and reach farthest
            if jump_ind == current_end:
                total_jumps += 1
                current_end = farthest_possible
        return total_jumps

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int jump(vector<int>& nums) {
        int totalJumps = 0, currentEnd = 0, farthestPossible = 0;
        for(int jumpI = 0; jumpI < nums.size() - 1; ++jumpI) {
            int jumpLen = nums[jumpI];
            // Update farthest index I can reach
            farthestPossible = max(farthestPossible, jumpI + jumpLen);
            // We have to use a new jump from any previous stair and reach farthest
            if(jumpI == currentEnd) {
                totalJumps++;
                currentEnd = farthestPossible;
            }
        }
        return totalJumps;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public int minJump(int[] nums) {
        int totalJumps = 0, currentEnd = 0, farthestPossible = 0;
        for(int jumpI = 0; jumpI < nums.length - 1; jumpI++) {
            int jumpLen = nums[jumpI];
            // Update farthest index I can reach
            farthestPossible = Math.max(farthestPossible, jumpI + jumpLen);
            // We have to use a new jump from any previous stair and reach farthest
            if(jumpI == currentEnd) {
                totalJumps++;
                currentEnd = farthestPossible;
            }
        }
        return totalJumps;
    }
}